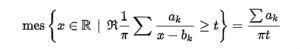George Boole (Born on November 2, 1815 – Died on December 8, 1864, in Ireland) was a Self-taught mathematician, philosopher, and logician. He was the inventor of Boolean algebra, which marks the foundations of modern computational arithmetic, Boole is regarded as one of the founders of the field of computer science.
In 1854 he published An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities, where he developed a system of rules that allowed him to express, manipulate and simplify logical and philosophical problems whose arguments admit two states (true or false) by mathematical procedures.
It could be said that he is the father of symbolic logical operators and that thanks to his algebra today it is possible to operate symbolically to perform logical operations.
Quick Facts Of George Boole
- Born: 2 November 1815, Lincoln, United Kingdom
- Famous For: English mathematician, and a founder of the algebraic tradition in logic
- Nationality: British
- Education: Bainbridge’s Commercial Academy
- Spouse: Mary Everest Boole (m. 1855–1864)
- Children: Ethel Lilian Voynich, Alicia Boole Stott, Lucy Everest Boole, Mary Ellen Boole Hinton, Margaret Taylor
- Region: Western philosophy
- Died: 8 December 1864, Ballintemple, Cork, Ireland
- Cause of Death: Pneumonia
- Burial: St Michael’s Church
- Awards: Royal Medal
Early Life Of George Boole
George Boole was born in Lincoln on November 2, 1815. He is the eldest son of John Boole and Mary Ann Joyce; very soon after, his sister Mary Ann was born, followed by William and Charles. John Boole is a shoemaker, his wife a chambermaid, he is passionate about science, literature, and mathematics.
In his store window, he proudly and enthusiastically displays a telescope he built. John Boole passed on to his son George “the love of study and books” and his passion for optics and astronomy, and they both made kaleidoscopes., sundials, and even trying to build a rudimentary calculating machine.
The income of the spouses barely allows enough to meet the needs of the family. George, therefore, studied in the local school and, in order to move up the social ladder, he studied Latin and Greek, while the bookseller William Brooke helped him in his study of Latin and also taught him the basics of grammar.
At the age of fourteen, he translated from Greek a poem Meleager, “Ode to Spring“, published in the Lincoln Herald, the local newspaper. His age is noted in the article, a teacher wrote the newspaper, not believing that a young boy is capable of such a translation.
This first controversy and the criticisms leveled at its translation prompted him to intensify his efforts to master ancient languages. After primary school, the only secondary education that a father can offer his eldest son is to follow, from September 10, 1828, courses taught at Thomas Bainbridge’s Commercial Academy in the City of Lincoln.
George made remarkable progress in mathematics there and concentrated especially on the study of algebraic equations. During his free time, he learns French, German, and Italian on his own, languages that will be useful for him to understand and develop his own mathematical ideas. Unfortunately, John Boole neglects his shoe repair business, which leads to bankruptcy.
George Boole Education
George Boole did not study for an academic degree, however, from the age of 16, he was an associate teacher at Heigham’s School in Doncaster. This was somewhat constrained on him since his dad’s business fell and he ended up supporting financially his parents, and siblings.
Mathematical Logic
George Boole was probably the first mathematician after John Wallis to turn to logical problems. The idea of applying the symbolic method to logic was first expressed by him in his article “Mathematical Analysis of Logic” (1847).
Dissatisfied with the results obtained in it, Boole expressed the desire that his views be judged on the basis of the extensive treatise “Investigation of the laws of thought, on which mathematical theories of logic and probability are based
Boole did not consider logic to be a branch of mathematics but found a deep analogy between the symbolic method of algebra and the symbolic method of representing logical forms and syllogisms.
By the unit, Boole denoted the universe of conceivable objects, by letter symbols – selections from it associated with ordinary adjectives and nouns (for example, if x = “horned” and y = “sheep”, the sequential choice of x and y from one will give the class of horned sheep).
Boole showed that symbolism of this kind obeys the same laws as algebraic, from which it followed that they can be added, subtracted, multiplied, and even divided. In such symbolism, statements can be reduced to the form of equations, and the conclusion from the two premises of the syllogism is obtained by eliminating the middle term according to the usual algebraic rules.
Even more original and remarkable was part of his system, presented in the “Laws of Thinking …”, forming a general symbolic method of logical inference. Boole showed how from any number of statements, including any number of terms, to deduce any conclusion following from these statements, by purely symbolic manipulations.
The second part of “The Laws of Thinking …” contains a similar attempt to find a general method in the calculus of probabilities, which allows, from the given probabilities of a set of events, to determine the probability of any other event logically connected with them.
Mathematical Analysis
In 1857, Boole published his treatise On the Comparison of Transcendents, with Certain Applications to the Theory of Definite Integrals (Compare transcendental with certain applications to the theory of definite integrals), where he studied the amount of waste a rational function. Among other results, he tested the so-called Boolean identity:
for any real numbers ak > 0, bk, and t > 0. 10 The generalization of this identity plays an important role in the theory of the Hilbert transform.
George Boole Death
On November 24, 1864, George Boole takes the road to Queen’s college from his house in Ballintemple, walking a distance of several kilometers. Torrential rainfalls and he leaves to teach his lessons. He arrives at college totally drenched, and comes home after class, in his wet clothes, and with a fever.
Bronchitis evolves into pleuropneumonia and he died the night of December 8, 1864. He is buried in the cemetery of Saint Michael’s Church in Blackrock (Cork) four days later. After George’s death, Mary Everest went to live in London where she died in 1916, at the age of 84.
George Boole Quotes
- It is not of the essence of mathematics to be conversant with the ideas of number and quantity. – George Boole
- No matter how correct a mathematical theorem may appear to be, one ought never to be satisfied that there was not something imperfect about it until it also gives the impression of being beautiful. – George Boole
- Of the many forms of false culture, a premature converse with abstractions is perhaps the most likely to prove fatal to the growth of a masculine vigor of intellect. – George Boole
- A successful attempt to express logical propositions by symbols, the laws of whose combinations should be founded upon the laws of the mental processes which they represent, would, so far, be a step towards a philosophical language. – George Boole
- That language is an instrument of human reason, and not merely a medium for the expression of thought, is a truth generally admitted. – George Boole
George Boole Books
- The Laws of Thought – 1854 (BUY LINK)
- The mathematical analysis of logic – 1847 (BUY LINK)
- Studies in logic and probability (BUY LINK)
- A Treatise on the Calculus of Finite Differences – 1860 (BUY LINK)
- Treatise on Differential Equations – 1859 (BUY LINK)
- Calculus of Finite Differences Fourth Edition (BUY LINK)